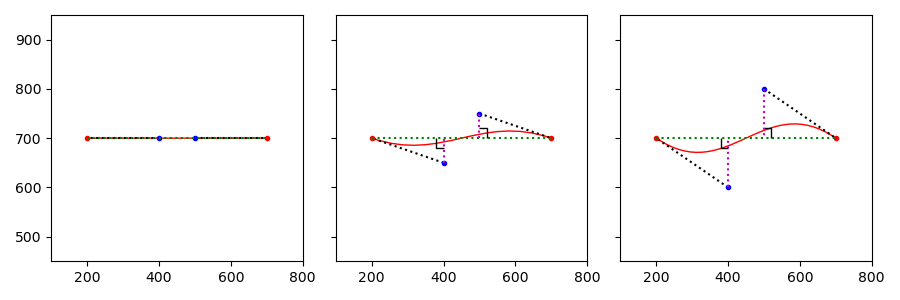
平直判断意义
绘制贝塞尔曲线时,通常用短线段连接而成,理论上线段越多越平滑。
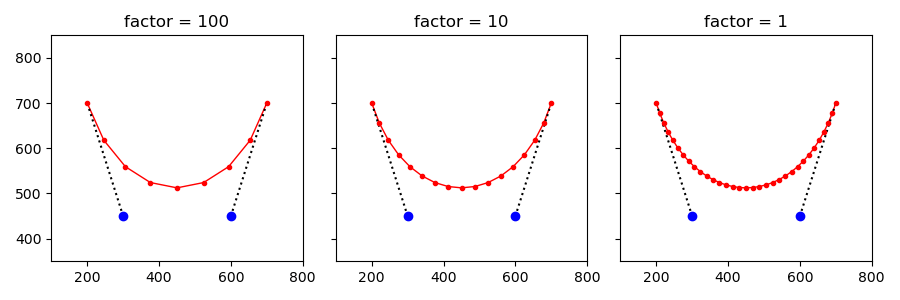
利用DeCasteljau算法可以将任意曲线细分成两段,继续递归细分直到满足合适的平滑度。
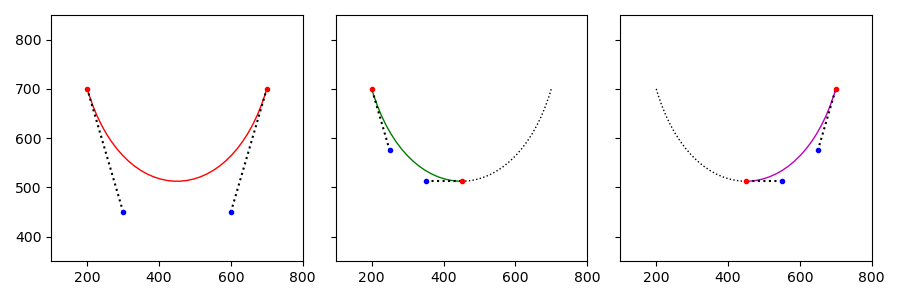
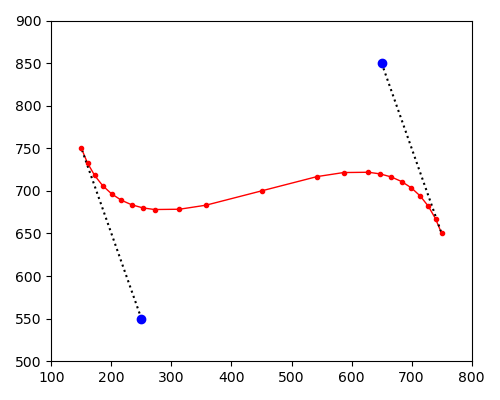
有必要评价细分后的贝塞尔曲线是否足够"直”,因为弯曲处需要密集的短线段,而平直处不需要。
向量叉积定义
向量叉积公式如下,即两个向量模长乘积,再乘以其夹角的sinθ值。
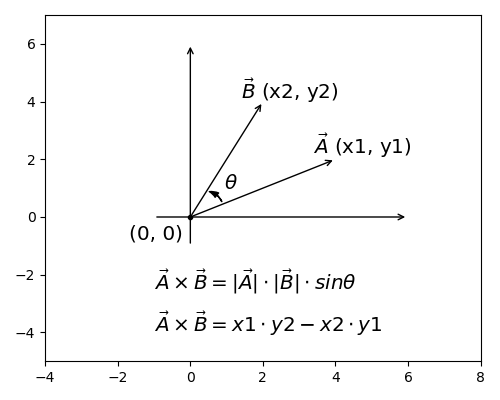
向量叉积也有另一种解读,表述为向量形成的平行四边形面积,用初中数学知识可证和上面公式是等价的。
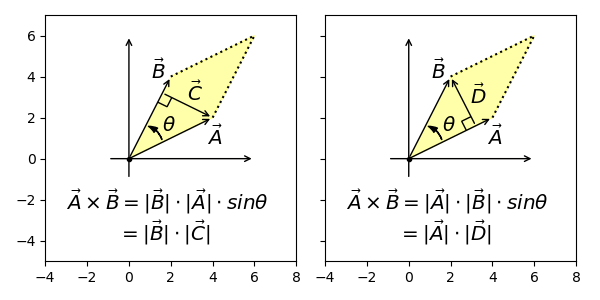
因为叉积公式有sinθ,所以两个向量形成的"面积"也带符号,简单总结为只有钝角或反向角的叉积都是负数。
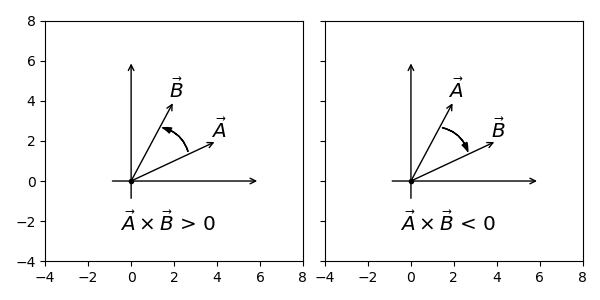
平直判断详解
回到最初的问题,以四阶贝塞尔曲线为例,需要判断曲线是否足够直。
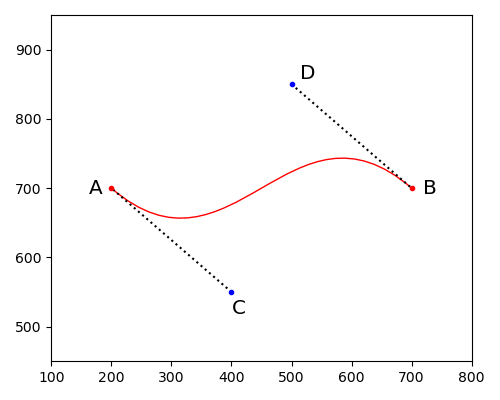
Brushes和nanovg都使用相同的算法,判断曲线足够直的表达式如下,其中k值是一个固定值。
$$ |\vec{AC} \times \vec{AB}| + |\vec{BD} \times \vec{AB}| < k \cdot |\vec{AB}| $$
回顾叉积定义是平行四边形面积,可以把上述表达式中的叉积解读为线段模长相乘。
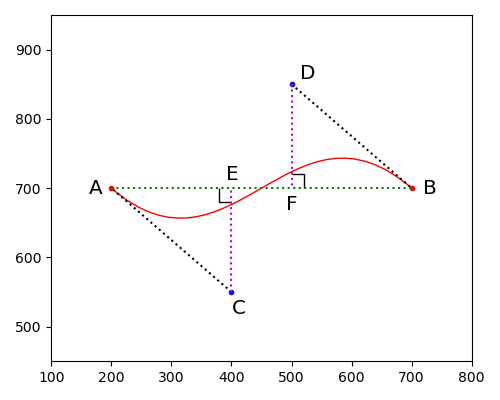
于是表达式转换如下,在进一步化简后,可以理解为比较控制点的偏离程度。
$$ |\vec{AC} \times \vec{AB}| + |\vec{BD} \times \vec{AB}| < k \cdot |\vec{AB}| $$
$$ |\vec{CE}| \cdot |\vec{AB}| + |\vec{DF}| \cdot |\vec{AB}| < k \cdot |\vec{AB}| $$
$$ (|\vec{CE}| + |\vec{DF}|) \cdot |\vec{AB}| < k \cdot |\vec{AB}| $$
$$ |\vec{CE}| + |\vec{DF}| < k $$
如果控制点没有偏离,贝塞尔曲线就退化为直线;偏离程度越大,弯曲程度也越大,也就更不适合以线段取代。